
Livre blanc sur le calcul d’intérêt
Par : Marc Gelinas, avocat, MBA
Président, Jurismedia Inc. / Margill
Texte originalement publié en anglais. La première version de 2008 fut publiée dans le magazine « REAL ESTATE LAW & INDUSTRY REPORT » (par Bureau of National Affaires, BNA)) Vol. 1, No. 4, 2008, pp 119-122. Le texte a été amélioré et développé davantage en avril 2020.By: Marc Gelinas, Attorney, MBA
CEO, Jurismedia Inc. / Margill
RÉSUMÉ : Au cours des 30 dernières années, les ordinateurs ont éliminé le besoin de comprendre les principes de base des intérêts. Par conséquent, de très nombreuses entreprises et d’organismes, petits et grands, ont oublié de nombreux principes fondamentaux, et les gens qui devraient savoir quelles normes et principes appliquer dans le calcul des intérêts se fient plutôt aux ordinateurs et, souvent, à d’anciens logiciels qui ne sont probablement plus en mesure de gérer les exigences complexes du marché d’aujourd’hui.
Cet article traite des principes fondamentaux du calcul des intérêt appliqué, notamment les méthodes de calcul d’intérêt simple, d’intérêt composé, du taux effectif et du taux d’intérêt majoré, la période de capitalisation ou composition, les principes de remboursement, le nombre de jours (Réel/Réel, 30/360, Réel/365, Réel/360), le taux effectif global (TEG)(TAC au Canada) et des situations plus complexes telles le nombre de semaines dans une année, le poids d’un mois dans une année et l’effet non-négligeable de l’année bissextile dans les calculs impliquant des montants plus importants.
Plus que des mathématiques
La science perdue du calcul d’intérêt
Rien ne semble plus simple, ou peu intéressant, que le calcul d’intérêt. En plus de votre bonne vieille calculatrice et de feuilles de calcul (telles qu’Excel), il existe des dizaines de logiciels pour calculer l’intérêt sur des prêts ou des hypothèques. Mais, fait surprenant, peu de ces solutions logicielles offrent des résultats précis dans des situations hors de l’ordinaire. Les gens qui comparent les résultats de leur banque avec ceux obtenus par le biais d’un logiciel gratuit ou peu coûteux sont toujours surpris de constater qu’ils ne sont pas pareils. Pourquoi? Est-ce qu’il existe une formule mathématique standard utilisée par tous et qui donne le bon résultat? La réponse est assez simple : oui et non.
Le coeur du problème : depuis des décennies, les ordinateurs ont éliminé le besoin de bien comprendre les principes fondamentaux des intérêts. Par conséquent, tellement d’entreprises et d’organismes ont oublié de nombreux principes de base, et les gens qui devraient savoir quels standards et principes appliquer dans le calcul des intérêts se fient plutôt aux ordinateurs et, souvent, à d »anciens logiciels qui ne sont probablement plus capables de gérer les exigences complexes du marché d’aujourd’hui.
Certaines lois nationales et communautaires (dont les Directives 87/102/CE (abrogée), 2008/48/CE en Europe, la loi Truth in Lending « TILA » aux États-Unis) et autres lois, règlements et « coutumes » nationales et régionales offrent quelques pistes par rapport à la marche à suivre pour les prêts à la consommation, mais laissent également énormément d’éléments à gérer par contrat. Par conséquent, cet article est destiné à fournir aux personnes qui dépendent de l’intérêt pour leur subsistance (banquiers, courtiers hypothécaires et autres prêteurs) et à celles pour qui l’intérêt est important (professionnels de l’immobilier, comptables, avocats, et autres professionnels de services financiers) un aperçu des subtilités et des écarts pouvant survenir lors de calculs d’intérêt. Le texte est divisé en quatre sections : définitions fondamentales, les bases de la base, les bases intermédiaires et les bases avancées.
Définitions fondamentales
Un prêt normal, de base, se compose de deux composantes : capital et intérêt. Tout semble assez simple. L’intérêt cependant, est tributaire d’une composante beaucoup plus complexe : le temps. Le temps ce sont les jours, les mois, les années et c’est le temps qui détermine le montant d’intérêt qui devient le nerf de la guerre des prêts. Il est ainsi important de bien comprendre ces quelques définitions fondamentales, plus qu’autrement, reliées au facteur temps.
Amortissement du prêt, versus terme du prêt :
- Amortissement : période requise afin de régler (réduire) progressivement le capital d’un prêt afin d’arriver à un solde de 0,00 (ou autre valeur résiduelle) en fin de prêt. La période d’amortissement prévoit un paiement en intérêt et en capital.
- Terme : temps qui s’écoule entre le début du prêt et sa fin, déterminé par entente entre le créancier et l’emprunteur.
- Exemple : une hypothèque peut être amortie sur 20 ans (240 mois) mais avoir un terme de 5 ans (60 mois), moment auquel les modalités de l’hypothèque doivent être renégociées.
Intérêts courus, versus intérêts échus, versus intérêts payés :
- Pour un comptable, la différence entre le couru et le payé est bien évidente mais pour des non-comptables, le concept est souvent mal compris. La différence entre les intérêts courus et les intérêts payés est particulièrement importante selon l’utilisation par le créancier d’une comptabilité d’exercice ou de caisse.
- Intérêt courus : intérêts acquis et non échus entre la date d’émission du prêt et la dernière date d’échéance des intérêts.
- Intérêts échus : intérêts courus qui doivent être immédiatement payés sans condition (aussi connu sous le terme intérêts en souffrance).
- Intérêts payés : intérêts courus et/ou échus qui sont réellement payés, donc monétairement, par l’emprunteur.
Taux d’intérêt nominal / taux d’intérêt effectif
- Taux d’intérêt nominal : taux d’intérêt coté pour du capital emprunté ou investi. Ne tient pas compte du facteur de composition ou de capitalisation des intérêts comme le fait le taux effectif.
- Taux d’intérêt effectif : véritable pourcentage d’intérêt qui est payé ou reçu sur une somme d’argent empruntée ou investie, par opposition au taux nominal. Le taux d’intérêt effectif tient compte du facteur de composition ou de capitalisation des intérêts. Attention, le taux d’intérêt effectif ne tient pas compte des frais chargés ou facturés à l’emprunteur dans un prêt qui font augmenter le taux de financement, ce dernier étant connu sous le terme, en Europe, Taux annuel (parfois le mot « actuariel » remplace « annuel ») effectif global (TAEG) comprenant les intérêts et les frais pour donner le rendement ou coût réel de prêt.
Capitalisation (composition) des intérêts
- Lorsque des intérêts sont échus, ceux-ci peuvent être capitalisés, soit ajoutés au solde servant à calculer les intérêts pour ainsi générer des intérêts. Strictement parlant, les intérêts non payés et ainsi capitalisés ne sont pas ajoutés au capital. De l’intérêt même capitalisé, ne devient pas du capital. Ces intérêts servent à déterminer le « solde de calcul » qui lui permet de calculer les prochains intérêts courus. Ils sont comptabilisés de façon distincte du capital pur, comptable.
- Attention, dans la définition ci-dessus, aux termes « lorsque des intérêts sont échus », car la fréquence de composition dans certaines méthodes de calcul d’intérêt que nous verrons ci-dessous, n’a aucun lien avec le paiement ou non les intérêts courus. La fréquence de composition sert à déterminer le « taux d’intérêt effectif » et même dans un prêt dans lequel les intérêts sont toujours payés tel que prévu dans l’échéancier, le total des intérêts courus sera plus élevé lorsque la composition est plus fréquente.
On pose aussi la question, doit-on dire UN intérêt ou DES intérêts? Selon diverses sources, on peut calculer l’intérêt ou LES intérêts d’un prêt. Donc, les deux peuvent être utilisés mais on doit dire des « taux d’intérêt » sans le s.
Les bases de la base
Intérêt simple ou composé ?
La distinction entre l’intérêt simple et l’intérêt composé est fort simple : en intérêt simple, aucun intérêt ne court sur les intérêts. Donc, tant que le capital ne baisse ou n’augmente pas, l’intérêt calculé à chaque jour restera inchangé. On peut comprendre que si ces intérêts courus ne sont payés par l’emprunteur qu’à une date lointaine, le créancier devient grandement perdant.
En intérêt composé, les intérêts courus portent intérêt. Donc, même si l’emprunteur ne paie les intérêts qu’à une date lointaine, le créancier aura profité d’intérêt additionnel sur ces intérêts et ne sera pas pénalisé par l’effet de l’inflation, essentiellement réduisant la valeur de son capital.
Ma fortune provient d’une combinaison du fait que je vis en Amérique, de certains gènes chanceux et de l’intérêt composé.
– Warren Buffett
L’intérêt composé est donc une méthode beaucoup plus équitable pour tous même si l’on voit souvent des lois, des règlements, des jurisprudences et des coutumes qui énoncent que l’intérêt simple doit être utilisé comme méthode à moins que l’entente ou le contrat indique spécifiquement qu’il s’agit d’intérêt composé.
L’intérêt simple est souvent utilisé par des prêteurs ou investisseurs ayant moins d’expérience puisque le calcul de l’intérêt simple se fait très facilement. La formule pour des périodes complètes :
Capital * taux d’intérêt de période * nombre de périodes = intérêt
Exemple : 10 000 * 1% par mois * 6 mois = 600,00
Évidemment, le calcul devient légèrement plus complexe lorsqu’on a des périodes qui ne sont pas complètes.
Alors on fait le calcul en tenant compte des jours :
Capital * taux d’intérêt annuel * nombre de jours / jours par année = intérêt
Exemple : 10 000 * 12% annuel * 182 jours / 365 jours par année = 598,26
On remarque déjà une différence du total de l’intérêt entre l’utilisation de périodes complètes versus le nombre de jours. On doit aussi se poser la question à savoir si une année est de 365, de 366 jours, de 365,25 ou encore que 360 jours (voir section « Comptage de jours »).
La plupart des prêts normaux à moyen ou long terme accordés par des banques, aux consommateurs ou aux entreprises sont calculés en intérêt composé. Un prêteur sophistiqué, telle une banque, comprend que le risque en intérêt composé est moindre qu’un prêt en intérêt simple puisque si l’emprunteur ne paie pas les intérêts, que ceux-ci généreront du revenu additionnel, à condition évidemment que la créance ne devienne irrécouvrable.
Pour les prêts personnels et commerciaux à court terme, souvent accordés par des entreprises de financement autres que les banques, on voit généralement que de l’intérêt simple est utilisé. Pourquoi ? Selon moi, car le calcul se fait facilement, à tort ou à raison, en calculant par le nombre de périodes (prêt de 3 mois, 2% par mois et le tour est joué : les intérêts sont les mêmes pour chacun des trois mois). Ces entreprises réalisent rapidement la faille de cette méthode trop simple lorsque le prêt est payé à l’avance ou en retard dans quel cas ils doivent changer leur méthode de calcul vers des jours exacts. Même les prêts à plus long terme accordés par prêteurs autres que des banques sont souvent consentis en intérêt simple, mais tel ne devra pas être la norme.
L’intérêt simple est généralement utilisé dans le domaine juridique, notamment en matière de responsabilité civile, mais encore là, les tribunaux envisagent de plus en plus les intérêts composés, qui reflètent plus précisément la « vraie vie ».
Méthode du taux effectif vs. Intérêt simple Capitalisé
L’intérêt composé peut être calculé de différentes façons : la méthode du « taux effectif » (certains l’appellent la méthode « actuarielle ») et la méthode de l’«intérêt simple capitalisé ». Généralement, ces deux méthodes donneront des résultats égaux pour des prêts réguliers (paiements réguliers à des dates régulières et respectées) mais tout événement irrégulier (paiement à l’avance ou en retard par exemple) génèrera un total d’intérêt légèrement différent selon la méthode utilisée. Même si les différences sont peu élevées, un conflit pourrait résulter entre prêteur et emprunteur à savoir qui a raison. Nous avons vu des situations où créancier et débiteur n’étaient pas d’accord avec les soldes obtenus par l’autre et qu’en bout de ligne ni un ni l’autre ne voulait changer sa méthode pour quelques dizaines ou centaines de dollars. Les seuls gagnants étaient les avocats!
L’intérêt simple capitalisé est une méthode facile de calculer l’intérêt (souvent utilisé dans les feuilles de calcul). Avec cette méthode, le même montant d’intérêt est calculé pour une période donnée et lorsqu’arrive le moment, la date, de capitalisation (ou composition), le total des intérêts générés, et non payés, est ajouté au solde. Ce solde devient le nouveau capital sur lequel les intérêts sont calculés jusqu’à la prochaine période de capitalisation. Cette méthode est en réalité de l’intérêt simple entrecoupé de capitalisation des intérêts à des périodes régulières ou non.
Pour reprendre notre exemple ci-dessus avec capitalisation mensuelle :
Mois 1 : 10 000,00 * 1% mensuel * 1 mois = 100,00
Mois 2 : 10 100,00 * 1% * 1 = 101,00
Mois 3 : 10 201,00 * 1% * 1 = 102,01
Mois 4 : 10 303,01 * 1% * 1 = 103,03
Mois 5 : 10 406,04 * 1% * 1 = 104,05
Mois 6 : 10 510,10 * 1% * 1 = 105,10
Total : 615,19
Si l’intérêt est payé à chaque « anniversaire » de capitalisation, on se retrouve alors en intérêt simple. Le facteur de capitalisation disparaît.
La méthode du taux effectif, quant à elle, permet d’effectuer le calcul en une seule opération selon une formule légèrement exponentielle qui tient compte du taux nominal, devenu effectif à cause de la fréquence de composition. Les intérêts générés quotidiennement au début d’une période sont inférieurs à ceux générés quotidiennement plus tard dans le prêt. Donc, le total quotidien d’intérêt change de jour en jour.
Formule de base pour périodes complètes :
Intérêt = Capital × [(1 + i/n)^(n×t) − 1] – Capital
i = taux d’intérêt nominal annuel
n = fréquence de périodes de composition
t = temps en nombre de périodes de l’emprunt
Notre exemple :
Intérêt = 10 000 × [(1 + 0,12/12)^(0,5×12) − 1]
Intérêt = 615,20
On remarque ici que le montant d’intérêt calculé selon la méthode du taux effectif donne le même résultat que le calcul en intérêt simple capitalisé car le calcul est parfaitement régulier et pour des périodes complètes. Les deux méthodes ne donneront pas les mêmes résultats dans des scénarios irréguliers.
Tout en demeurant inchangée au niveau mathématique, la formule du taux effectif devient beaucoup plus complexe pour des fractions de périodes, pour tenir compte de périodes irrégulières. Des logiciels plus sophistiqués sont ainsi requis qui tiennent compte de fractions de périodes.
Pour les prêts calculés selon la méthode intérêt simple capitalisé, l’emprunteur paie plus d’intérêt au cours des premiers mois que ce qui aurait été payé en utilisant la méthode du taux effectif. La méthode du taux effectif traite à la fois l’emprunteur et le prêteur de façon équitable et un nombre croissant de juridictions ont, et exigent, que les prêts à la consommation utilisent cette méthode.

Période de capitalisation / composition
Lorsqu’on parle d’intérêt composé ou capitalisé, l’on doit donner la fréquence de cette capitalisation (annuelle, mensuelle, quotidienne, etc.). La fréquence varie en fonction du type de prêt, de certaines lois et des pratiques dans l’industrie. Le taux d’intérêt chargé (ou taux effectif) est plus élevé lorsque la période de capitalisation est quotidienne et il diminue à mesure que la période s’allonge : hebdomadaire, aux deux semaines, mensuelle (hypothèques dans la plupart des pays), trimestrielle, semestrielle (hypothèques au Canada) et annuelle.
Dans un contrat de prêt, le taux d’intérêt dit « nominal » est généralement le seul divulgué tout en indiquant également la fréquence de capitalisation qui détermine le taux effectif (ou réel).
| Taux nominal : | 12 % | 30 % |
| Taux effectif | ||
| Composé annuellement | 12,0000 % | 30,0000 % |
| Composé semestriellement | 12,3600 % | 32,2500 % |
| Composé mensuellement | 12,6825 % | 34,4889 % |
| Composé quotidiennement | 12,7475 % | 34,9692 % |
Divulguer le taux effectif donnerait, bien entendu, une idée plus précise du coût réel d’un prêt pour les consommateurs (nous discuterons du taux d’intérêt « réellement réel » plus tard connu sous le terme Taux annuel effectif global (TAEG) en Europe qui tient compte des frais facturés dans le prêt et de la capitalisation.
Qu’en est-il de la méthode du taux d’intérêt majoré (en anglais : Add-on interest)? Mirage de faible taux d’intérêt…
Aussi connu sous le terme intérêt « pré-calculé » ou encore « méthode du taux forfaitaire », l’intérêt total calculé selon la méthode expliquée ci-dessous, est « ajouté » au capital d’origine et le résultat est simplement divisé par le nombre de paiements à effectuer. Cette méthode permet des calculs simples et est souvent utilisée pour le financement de véhicules et dans le microcrédit. Cependant, l’acheteur n’est pas toujours conscient que les intérêts facturés équivalent presque au double du taux indiqué.
Les intérêts majorés fonctionnent comme suit : un taux de 12,50 $ (ou €, F, £ ou autre monnaie) pour cent par année (ou 12,5%) prélevé sur un prêt de 20 000 $ à être remboursé par versements mensuels pendant 4 ans, donnera un total d’intérêts de 10 000 $ (20 000/100 * 12,50 * 4). Le prêt total est donc 30 000 $ à rembourser en 48 versements égaux de 625,00 $.
Plusieurs ont du mal à comprendre que le taux, qui semble raisonnable lorsque divulgué comme montant d’intérêt ou en pourcentage, est en fait très loin du taux réel de coût d’emprunt (TEG en Europe, TAC au Canada) devant être divulgué selon la loi, car les intérêts majorés ne tiennent pas compte de l’amortissement (ou réduction progressive) du capital à chacun des paiements. La divulgation du TEG/TAC et les lois qui fixent le taux d’intérêt maximum pouvant légalement être facturés aux consommateurs, exigent que les taux calculés et divulgués soient précis du point de vue mathématique.
À l’exception de certains scénarios (paiement que des intérêts courus et lorsque les paiements sont insuffisants pour rembourser la portion intérêt), lorsqu’un paiement est effectué, le capital et les intérêts sont généralement remboursés. Néanmoins, avec la méthode des intérêts majorés, le 12,50% est toujours facturé sur le capital d’origine, peu importe le capital remboursé par l’emprunteur au créancier. Après 6 mois, si 1500 $ en capital a été remboursé au créancier, ce dernier peut prêter ce montant et en profiter à nouveau alors que l’emprunteur lui, continue de payer des intérêts sur le montant du capital initial.
Un autre problème surgit lorsque l’emprunteur manque un paiement. Est-ce que de l’intérêt serait ajouté sur ce montant ? Si oui, le double en intérêt serait alors facturé.
Dans notre exemple ci-dessus, qui indique un taux majoré de 12,5%, le taux effectif annuel est en réalité plus de 21,5%.
Règle de 72, Règle de 78
Comme ces règles ont été créées avant l’arrivée de l’ordinateur, elles sont maintenant désuètes et ces méthodes de « raccourci » ne seront pas traitées dans cet article. Ces méthodes de calcul ne devraient plus être utilisées depuis longtemps. Elles ont été élaborées simplement pour estimer mais ne peuvent être utilisées pour obtenir des données précises.
Date d’origine, date d’échéance
Dans un prêt, il peut être difficile de décider si l’on inclut la date de fin de prêt (échéance) dans le calcul de l’intérêt. Généralement, sauf pour quelques exceptions dans certains pays, le jour d’échéance n’est pas compté lors du calcul des jours d’un prêt – seul le nombre de jours écoulés est compté. La logique est assez simple, comme l’illustre cet exemple. Combien d’intérêt est payable sur un prêt de 10 000 $ pour un jour? Avec la date d’origine (aussi connu sous le terme date de valeur) du prêt est le 1er avril, est-ce que la date d’échéance sera le 1er avril ou le 2 avril ? Cette dernière est plus logique, car elle prend en compte la totalité du 1er avril à minuit (disons moins une fraction de seconde), et un seul jour d’intérêt est dû.
Nous avons également vu le scénario inverse où les intérêts courus de la date d’origine doivent être exclus du calcul mais ceux de la date de fin inclus. À notre avis, cette méthode est moins commune et ne devrait pas être utilisée. Il peut s’agir d’une entente entre les parties qui décident ainsi, et l’on pourrait argumenter que le prêt est fait en fin de journée et remboursé en début de journée pour justifier cette méthode mais ceci n’est pas la norme.
Cette problématique d’inclusion ou d’exclusion de date finale mène à d’importantes erreurs dans des feuilles de calcul qui oublient le dernier jour d’intérêt de l’année (généralement le 31 décembre) puisque le calcul est incorrectement fait au 31 le matin (0h00) et non à minuit (ou 0h00 le 1er janvier). Des millions de dollars sont perdus (et gagnés par l’autre partie) à chaque année à cause d’un oubli à ce niveau. Il est donc primordial de vérifier que le dernier jour de l’année ou du mois est bien comptabilisé (et facturé à l’emprunteur) dans les calculs.
Voir le texte (en anglais seulement) : Loan Servicing with Excel? Pitfalls and alternatives
Bases intermédiaires
Comptage de jours
Le comptage de jours est la méthode par laquelle le nombre de jours entre deux dates (date d’origine du prêt, dates de paiement (coupon), date de fin du prêt) est calculé. Même si la pratique ne reflète aucunement la théorie, tous les prêts, hypothèques et obligations devraient spécifier le comptage de jours qui est utilisé pour le calcul des intérêts. Cela peut sembler simple, mais il n’existe pas moins de 20 méthodes de comptage de jour, dépendant du pays, de l’industrie, du type de client et du type d’instrument financier!
Les quatre méthodes les plus communes pour le comptage de jours sont décrites ci-dessous. Selon le pays et l’industrie, il peut y avoir des variantes dans les noms utilisés. Ces noms suivent la nomenclature ISO 15022 :
- Réel/Réel, parfois aussi appelé Réel/365 (ISDA), est la méthode de comptage de jours la plus intuitive et la plus précise. Pour déterminer le nombre de jours entre deux dates, le nombre réel de jours, y compris l’effet d’une année bissextile, est compté. Cette méthode est utilisée pour les bons du Trésor et les billets, et sauf indication contraire dans la loi, le contrat ou la « coutume », elle devrait être utilisée pour une précision maximale, tout en sachant qu’elle est relativement difficile à appliquer dans des feuilles de calcul tel qu’on le verra dans la section « Bases avancées ».
- La méthode 30/360 a été inventée à la veille de l’arrivée des ordinateurs pour faciliter les calculs. Dans cette méthode, tous les mois, y compris février, ont 30 jours, et toutes les années ont 360 jours. Sans un logiciel sophistiqué de calcul, cette méthode devient complexe à gérer pour des prêts irréguliers comme le reflète cet exemple : le nombre de jours lors d’une année bissextile, entre le 1er février, et le 28 février (à 0h00) est de 27 alors que le nombre de jours du 1er février au 29 février (à 0h00) est de 29 jours, soit deux jours de plus pour la journée additionnelle. Diverses sous-méthodes, dont la méthode 30/360 U ont été élaborées pour compter les jours différemment surtout pour le mois de février.
- La méthode Réel/365 (fixe) compte le nombre réel de jours d’un prêt, mais le dénominateur (utilisé pour calculer un taux d’intérêt quotidien) exclura le jour supplémentaire d’une année bissextile. Ainsi, un taux d’intérêt quotidien est toujours au taux annuel divisé par 365 (pour un calcul en intérêt simple).
- Réel/360 est une méthode un peu étrange, qui compte le nombre réel de jours pendant lesquels un prêt est en cours et calcule le taux d’intérêt sur la base d’une année de 360 jours. Ainsi, sur un an, un prêt de 1000 $ à 10% rapportera 101,39 $ en intérêts (365/360) et non le rendement annuel auquel on aurait pu s’attendre de 100 $ exactement. Cette méthode profite évidemment au prêteur. On voit cette méthode surtout aux États-Unis et sur le marché monétaire de la zone Euro.
Taux effectif global (TEG/TAEG) et Taux annuel du coût d’emprunt (TAC)
Le TEG (en Europe) (ou TAC au Canada) est un taux « standardisé » (en pourcentage), qui prend en compte tous les frais de financement (intérêt et frais) obligatoires associés à un prêt. Il est couramment utilisé pour comparer les prêts offerts par différents prêteurs. La plupart des juridictions occidentales obligent légalement les sociétés offrant de prêts aux consommateurs et des hypothèques de dévoiler le TEG lorsqu’ils affichent un taux.
Le TEG démontre le coût réel du prêt. Il prend en compte les frais de financement, composé de l’intérêt et des autres frais obligatoires, qui doivent être payés par l’emprunteur tout au long du prêt. Les frais payés au début du prêt auront un effet différent sur le TEG comparativement à s’ils étaient payés à la fin du prêt ou payés mensuellement. Certains frais sont financés dans le prêt et vont générer à leur tour des intérêts. Ceci est également pris en compte dans le calcul du TEG. Si des montants forfaitaires sont versés, ils affecteront également le TEG, car ils réduisent les coûts en intérêt.
Il existe de nombreux logiciels de calcul des intérêts, beaucoup de méthodes de calcul des intérêts pour l’amortissement et, malheureusement, diverses formules TEG. Les différences dans les résultats obtenus avec ces méthodes sont généralement assez faibles et, on l’espère, respectent une précision acceptable de 1/8% à 1/4% (transactions irrégulières) habituellement exigée par la loi.
Dans certains pays, comme la France, la loi prévoit des sanctions sévères en cas de divulgation inexacte du TEG : les intérêts sur les crédits à la consommation étant réduits à 0% et l’application d’un taux d’intérêt légal très bas sur les crédits commerciaux. Conclusion : ne négligez pas le calcul du TEG!
Malheureusement, il existe aussi de nombreux types de TEG : actuariel, nominal, effectif, réel et historique. Ainsi, il n’est pas toujours facile de naviguer dans ces eaux. Aux États-Unis, le TEG (APR – Annual Percentage Rate) ne tient compte que du taux d’intérêt nominal (et non du taux effectif) et des frais obligatoires. Des efforts ont été déployés pour standardiser le TEG, mais la résistance est forte. Changer quelque chose qui prête déjà à la confusion pourrait encore plus embrouiller les consommateurs. En Europe, des normes plus strictes ont été appliquées puisqu’un véritable TEG doit être utilisé : le « TEG effectif » qui prend en compte tous les frais obligatoires ainsi que le taux d’intérêt effectif (et non nominal). Le TEG effectif est en fait connu sous le nom TAEG (taux annuel effectif global en France ou taux actuariel effectif global en Europe)(en anglais Annual Percentage Yield ou APY).
Séquence de remboursement des composantes d’un prêt : Capital, intérêts et frais
Fondamentalement, que ce soit en intérêt simple ou en intérêt composé, les intérêts accumulés sont généralement remboursés avant le capital. Ce n’est que lorsque le paiement est supérieur au total des intérêts accumulés que le solde en capital sera réduit. On dit que les intérêts sont calculés et payés non à l’avance (autres termes : intérêts payés à l’échéance (IPE), intérêts post-comptés, intérêts à terme échu ou taux in fine) par opposition à la méthode moins commune par laquelle les intérêts sont calculés et payés à l’avance (IPA) (autres termes : intérêts précomptés, intérêts à terme à échoir).
Évidemment, la méthode plus commune de payer des intérêts courus avant le capital n’est pas toujours respectée et nous voyons souvent des situations dans lesquelles du capital est remboursé avant que les intérêts échus et courus le soient. En intérêt simple, ceci procure un avantage important à l’emprunteur puisque les intérêts échus ne portent pas intérêt. En intérêt composé (méthode du taux effectif), les intérêts portent intérêt et donc que le capital soit payé en premier ou non, l’effet ne sera que sur les aspects comptables et non mathématiques.
Finalement, lorsque des frais sont facturés en sus des intérêts, ceux-ci sont généralement payés ou remboursés avant les intérêts et le capital. Ceci n’est pas universel et encore, certaines juridictions, surtout en créances de type juridique, vont obliger que le capital soit payé avant les intérêts ou frais. On ne voit donc pas de réels standards à cet égard.
Bases avancées
Cette section est dédiée aux subtilités qui peuvent produire des différences mineures dans les totaux des intérêts, souvent à l’intérieur des marges d’erreur autorisées. Trop souvent, la cause de ces écarts provient du fait que le logiciel de calcul utilisé est incapable de gérer ces subtilités.
Calcul de périodes d’une année
La mathématique derrière le calcul des intérêts et le calendrier d’amortissement nécessitent que le nombre de périodes dans une année soit connu. Cela peut sembler assez simple, mais il existe des zones grises.
– Nombre de semaines dans une année
Dans le calcul de l’amortissement, lorsque le paiement ou la période de composition est hebdomadaire, aux deux semaines ou à toutes les quatre semaines, différents logiciels utiliseront différents nombres de périodes par année.
Par exemple, dans une année, les paiements ou la composition hebdomadaire sont de 52 fois par année, ou 52,143 fois (365/7) ou même 52,286 (366/7) fois.
Bien qu’il existe peu de normes et que les différences entre les résultats soient assez faibles, le logiciel devrait inclure ces options.
– Poids relatif des mois
La logique nous indique qu’un mois est 1/12 (0,0833) d’une année et que les intérêts pour un mois complet devraient être cette fraction.
Une autre possibilité consiste à baser l’intérêt sur le nombre de jours de chaque mois. Selon cette méthode, janvier compterait pour un peu plus d’un douzième : 31/365 (0,0849) – ou 31/366 (0,0847) dans une année bissextile, si le nombre de jours est Réel/Réel. Alors, qu’en est-il de février ? Faut-il payer moins d’intérêt en février que dans un mois de 31 jours ? En utilisant cette méthode, la réponse est oui.
En général, dans les calculs réguliers avec paiements réguliers, la première méthode est beaucoup plus utilisée, mais les deux méthodes sont acceptables.
Dénominateur basé sur l’année
Lorsque vous utilisez la méthode Réel/Réel pour le calcul en intérêt simple afin de déterminer les intérêts sur un prêt ou pour une période du prêt (formule : solde du capital * taux d’intérêt annuel * nombre de jours/nombre de jours dans une année), l’année bissextile a un effet subtil sur le « nombre de jours » (le dénominateur). Diverses méthodes sont utilisées pour déterminer si ce sera 365 ou 366 jours.
Une méthode divise le calcul pour tenir compte, comme référence, de l’année civile. L’exemple du Tableau 1 illustre la méthode de calcul selon laquelle les intérêts accumulés du 1er novembre 2019 au 1er décembre 2019 sont le capital (ou solde) * le taux d’intérêt annuel * 30/365. Cette méthode s’appelle ISDA (International Swaps and Derivatives Association).
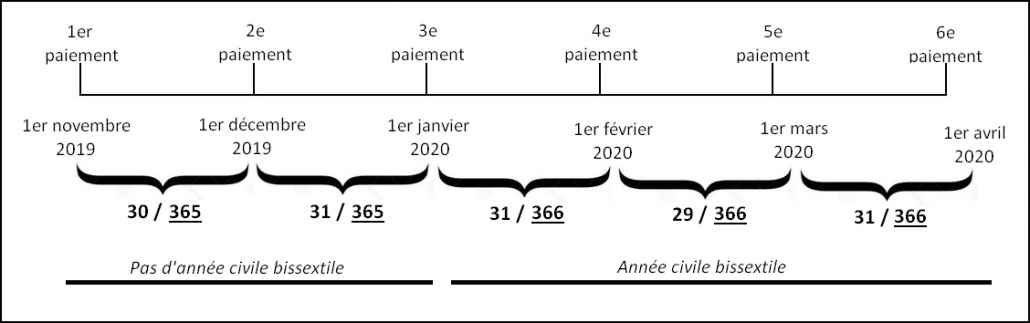
Une deuxième méthode, un peu plus complexe, prend en compte la date anniversaire de paiement pour calculer l’année de base. L’exemple dans le Tableau 2 démontre la méthode de calcul selon laquelle, en comptant à rebours, le nombre de jours est pris en compte entre la fin de la période de paiement réelle et l’année précédente. Pour les intérêts accumulés du 1er novembre 2019 au 1er décembre 2019, cette méthode tiendra compte de la date anniversaire (de décembre 2019 à décembre 2018, à rebours) pour calculer le nombre de jours de cette année-là. Puisqu’il y a 365 jours dans cette période, 365 sera utilisé comme base. Pour la période du 1er mars 2020 au 1er avril 2020, la base de 366 sera également utilisée car du 1er avril 2020 au 1er avril 2019 (en comptant à rebours), il y a 366 jours.
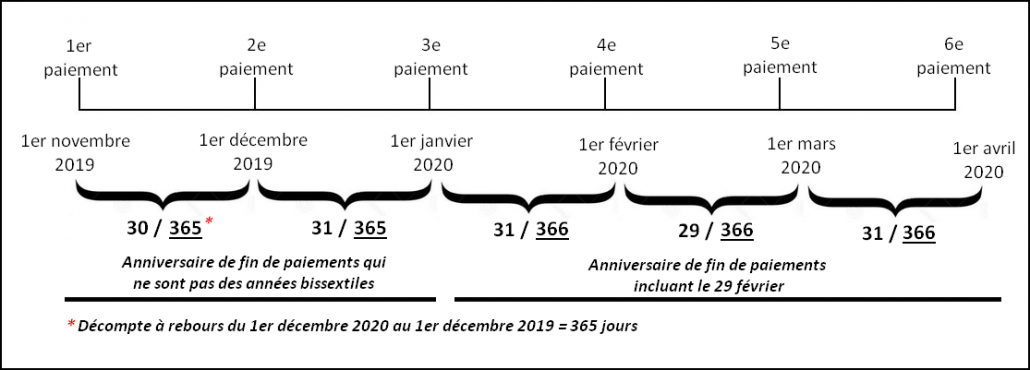
Dans le marché financier, d’autres méthodes incluent l’ISMA (International Securities Markets Association) et l’AFB (Association Française de Banques), qui empruntent des aspects des méthodes ci-dessus mais avec certaines subtilités qui ne seront pas analysées ici.
Périodes dites « courtes » et « longues » en intérêt composé
Enfin, une situation particulière qui reflète probablement un manque d’outils de calcul dans un passé lointain est encore utilisée aujourd’hui. Dans certaines juridictions, lorsqu’un paiement sur un prêt à intérêt composé régulier (méthode du taux effectif) est irrégulier ou en retard, la méthode de l’intérêt simple est utilisée pour calculer l’intérêt pour la période. Nous voyons souvent ceci dans les hypothèques lorsque le premier paiement n’est pas payé exactement une période normale (paiements mensuels habituellement) après la date d’origine. Par exemple, un prêt débute le 12 mars et le premier paiement devra être fait par l’emprunteur le 1 avril. La période entre ces dates est considérée une période « courte » et les intérêts seront calculés en intérêt simple pour ces 20 jours (12 mars à 0h00 au 31 mars à minuit). En revanche, pour un prêt débutant le 12 mars avec le premier paiement (en capital et intérêts) le 1 mai, cette période sera considérée une période « longue » ou encore composé d’une période courte et d’une période normale. Certains prêteurs ajouteront un paiement le 1 avril qui ne paiera que les intérêts. Le calcul de ces intérêts de 20 jours sera effectué en intérêt simple. Ce paiement additionnel est appelé « Date d’ajustement des intérêts » et permet conséquemment d’ignorer ce paiement afin de générer un échéancier régulier et standard pouvant être calculé avec des applications peu sophistiquées et même avec les tables d’amortissement papier (ces anciens livrets qui comprenaient une multitude de montants empruntés, taux et années d’amortissement pour obtenir le paiement mensuel!).
Une autre situation où l’on voit ceci par exemple, si un paiement est dû le 1er du mois mais n’est payé que le 12 du mois, les intérêts seraient calculés en intérêt simple comme suit : (solde * taux du jour * 12/31) + (solde * taux du jour * 19/31) pour cette période seulement. Bien qu’il soit historiquement compréhensible et que la différence entre les deux méthodes soit assez petite, nous trouvons ce changement soudain de méthode maladroit et difficile à justifier à l’ère de l’informatique. La méthode du taux effectif, quant à elle, continuerait de calculer les intérêts normalement pour cette période, avec la formule prescrite (exponentielle exposée dans une section ci-dessus) tout en calculant les jours courus et en créant des périodes de référence afin de compléter la variable « t » (temps en nombre de périodes de l’emprunt) de la formule.
Conclusion
Cette enquête a mis en évidence les sources de confusion généralisée que j’ai observées pendant de nombreuses années en étudiant les principes d’intérêt appliqué, en travaillant avec les clients et en voyant ce que le marché a à offrir en termes de solutions. Il est à espérer que, lorsque les chiffres ne concordent tout simplement pas, ces principes de base orienteront le professionnel concerné vers des solutions précises et satisfaisantes.
Lorsque la législation ne prévoit pas de solution, il faut être conscient des possibilités de divergences éventuelles. De plus, pour assurer une précision maximale dans le calcul d’intérêt, les éléments décrits ci-dessus devraient être inclus dans les paramètres de calcul décrits dans le contrat de prêt, comme cela se fait dans les grandes transactions internationales.
Bibliographie :
- Broverman, Samuel A, Mathematics of Investment and Credit, Second Edition, Actex Publications, 1996
- Chouinard, Pierre, Mathematics of Interest, 1990
- Code de commerce, France
- Cost of Borrowing (Banks) Regulations, Justice Canada, DORS/2001-101
- Directive 98/7/EEC, European Community
- Directive 87/102/EEC, European Community
- Kellison, Stephen G, The Theory of Interest, Irwin McGraw-Hill, 1991
- International Swaps and Derivatives Association web site: www.isda.org
- Late Payment of Commercial Debts (Interest Act), United Kingdom
- Margill, interest calculation, User’s Guide and web site www.margill.com
- Mayle, Jan, Standard Securities Calculation Methods, Volume 1, 3e édition, Securities Industry Association, 1996
- Ménard, Louise, Dictionnaire de la comptabilité et de la gestion financière, 3e édition
- SWX Swiss Exchange, Accrued Interest & Yield Calculations and Determination of Holiday Calendars
- Truth in Lending Act, Regulation Z, U.S. Federal Reserve Board
À propos de l’auteur
Marc Gélinas, avocat, MBA (Université McGill, promotion de 1994), est le fondateur et le PDG de Jurismedia, inc., développeur des logiciels Margill, solutions de calcul d’intérêt et de gestion de prêts utilisées par des milliers de prêteurs, comptables, banquiers, courtiers hypothécaires, professionnels de la location, avocats, juges, syndicats et planificateurs financiers dans plus de 40 pays. En tant qu’avocat, il a été appelé, au cours des 25 dernières années, à résoudre de nombreuses questions complexes concernant l’intérêt et son exactitude aux États-Unis, au Canada et en Europe.
Courriel : [email protected]